Aeromorph hinge behaviour
1112 wordsRecap of Paper’s Approach
In the Aeromorph paper, the authors describe a way to predict the bending angle $\theta$ of two inflated “airbags” connected by a common, inextensible seam. The seam’s initial width $w$ is preserved during inflation because the material cannot stretch. This geometric constraint means the bend angle will be the one that keeps the seam’s width exactly at $w$ when the two sides rotate relative to each other.
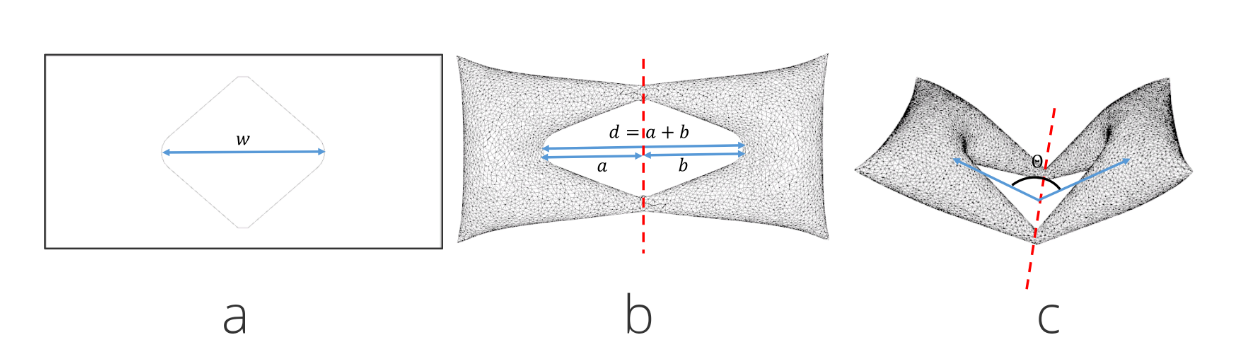
They model this setup as a triangle whose sides are:
- $a$ : distance from the hinge line to one seam tip
- $b$ : distance from the hinge line to the other seam tip
- $w$ : the seam width (fixed from the original design)
Using this model, the angle $\theta$ can be computed from the law of cosines:
\[\theta = \arccos\left(\frac{a^2 + b^2 - w^2}{2ab}\right)\]This equation finds the angle opposite the side $w$ in the triangle formed by the two seam tips and the hinge point.
Law of Cosines (Back to the Basics)
Before trying to reconcile the simulated results with the Aeromorph formula, it’s worth stepping back to recall how the law of cosines actually works — and why it needs to be applied with the correct definitions for $a$, $b$, and $w$ .
In standard triangle geometry, the law of cosines relates the lengths of all three sides of a triangle to one of its angles:
- Unknown side: $c = \sqrt{a^2 + b^2 - 2ab\cos\gamma}$
- Unknown angle: $\gamma = \arccos\left(\frac{a^2 + b^2 - c^2}{2ab}\right)$
The Aeromorph bending equation is simply the unknown angle form, where $w$ plays the role of the third side opposite the bending angle $\theta$.
The key point is that you need all three sides to apply this formula. If $a$ and $b$ are chosen so that $w = a + b$, the formula always produces $\theta = 180^\circ$; a flat, unbent configuration. In the Aeromorph context, $w$ is fixed by the design (the original seam width before inflation) and is assumed to remain unchanged as the structure bends. Using definitions of $a$, $b$, and $w$ that don’t match this setup will lead to unrealistic results.
To get a better sense of how diamond proportions affect bending, I did “manual” measurements using a set of photographs from the Aeromorph paper. Each image shows a different aspect ratio between the diamond’s horizontal ($x$) and vertical ($y$) axes. The values were extracted directly from the images, so they are approximate and subject to perspective and scaling differences, particularly since the top (flat) and bottom (inflated) rows are not to the same scale.
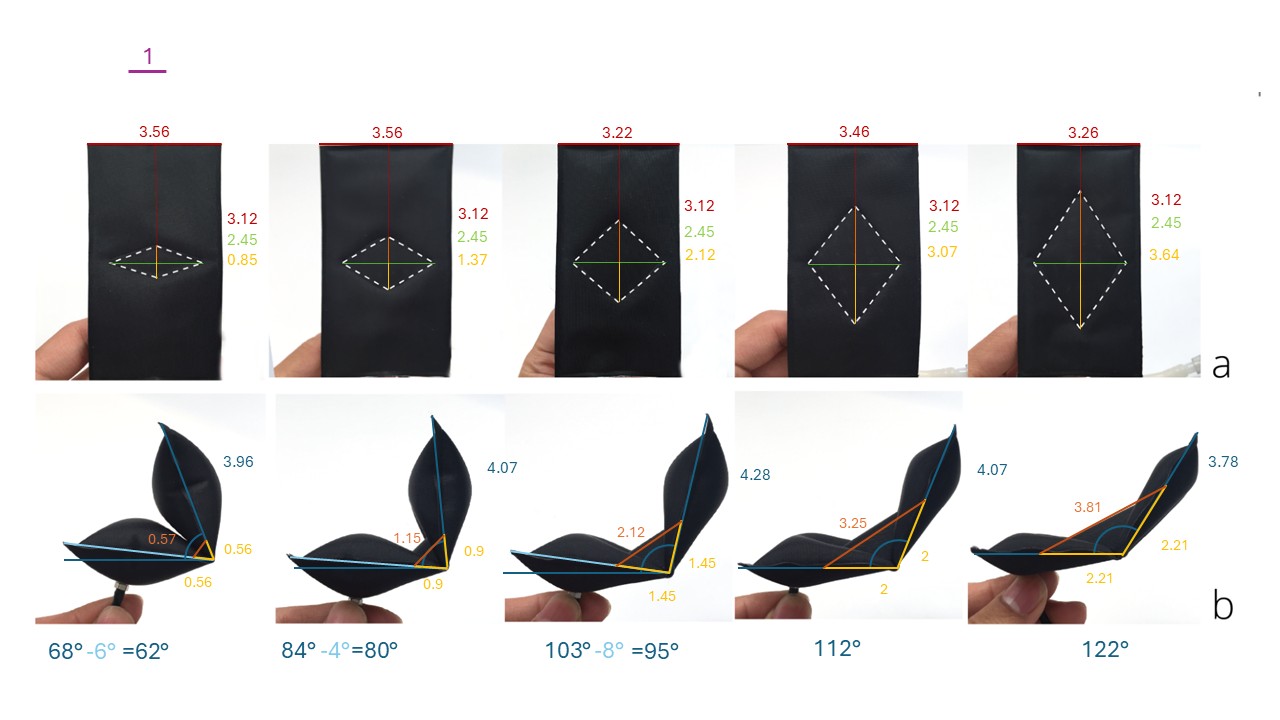
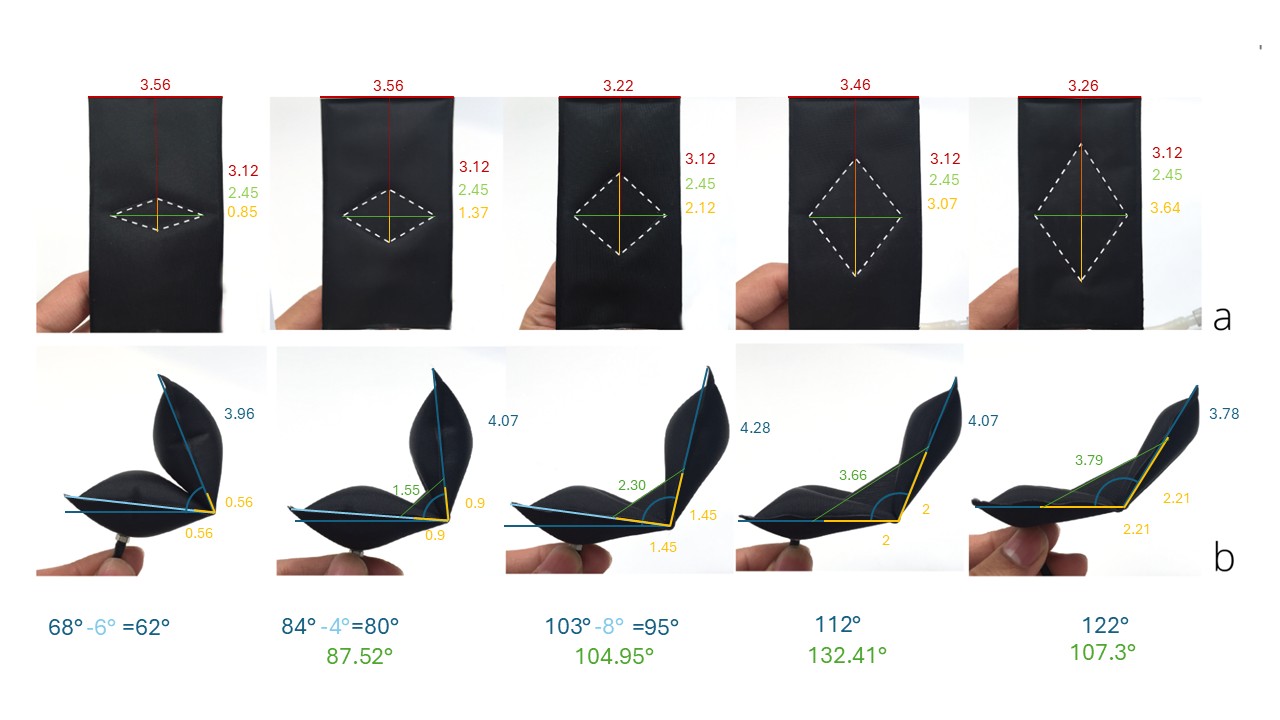
For the measurements, I took two approaches:
-
Figure 3: On the bottom (inflated) images, I scaled $a$ and $b$ and directly connected the seam tips, and manually measured $w$. I didn’t calculate $\theta$ as I’ve already measure it manually.
-
Figure 4: When the diamond’s $y$-axis was visible, I drew a line and extended it to the assumed edges of the pouches. In most cases, $a$ and $b$ would have to be extended to meet these points. In this case, I calculated $\theta$ using $a$ and $b$ as if they were inextensible, but substituted the newly measured $w$ from each image. The resulting angles are shown in green.
From these measurements, we can observe that the pouches are nearly square, with dimensions of approximately $3.\text{something} \times 3.12$ in all cases. This allows us to normalize the scale of the diamond’s $x$-axis (the one that remains constant) to $2.45$, assuming it represents $0.8$ of the pouch width.
With this normalization, we can establish a relationship between the diamond’s $x$- and $y$-axes and the resulting bending angle — either the one measured manually from the inflated images, or the one obtained using the law of cosines (assuming $a$ and $b$ are inextensible and using the measured $w$).
| $x\ axis$ | $y\ axis$ | $y/x$ | $y/x\ chosen$ | $fraction$ | $θ\ observed\ (°)$ | $diff\ (°)$ | $θ\ calculated\ (°)$ | $diff\ (°)$ |
|---|---|---|---|---|---|---|---|---|
| $2.45$ | $0.85$ | $0.347$ | $0.4$ | $\tfrac{2}{5}$ | $62$ | - | $62$ * | - |
| $2.45$ | $1.37$ | $0.559$ | $0.6$ | $\tfrac{2}{5}$ | $80$ | $18$ | $87.52$ | $25.52$ |
| $2.45$ | $2.12$ | $0.865$ | $0.8$ | $\tfrac{2}{5}$ | $95$ | $15$ | $104.95$ | $17.43$ |
| $2.45$ | $3.07$ | $1.253$ | $1.2$ | $\tfrac{2}{5}$ | $112$ | $17$ | $132.41$ | $27.46$ |
| $2.45$ | $3.64$ | $1.486$ | $1.4$ | $\tfrac{2}{5}$ | $122$ | $10$ | $107.30$ | $-25.11$ |
To compare my simulation results with the Aeromorph-style proportions, I first fitted two simple empirical models to my measurement data:
- Linear model: $\theta \approx 50.72 \cdot (y/x) + 48.45$
- Power-law model: $\theta \approx 101.76 \cdot (y/x)^{0.45}$
These models map the diamond aspect ratio $y/x$ directly to a bending angle without needing $a$, $b$, or $w$ separately. They aren’t intended as exact physics — only as quick trend fits to see whether the MeshFEM Inflatables simulations follow a similar relationship.
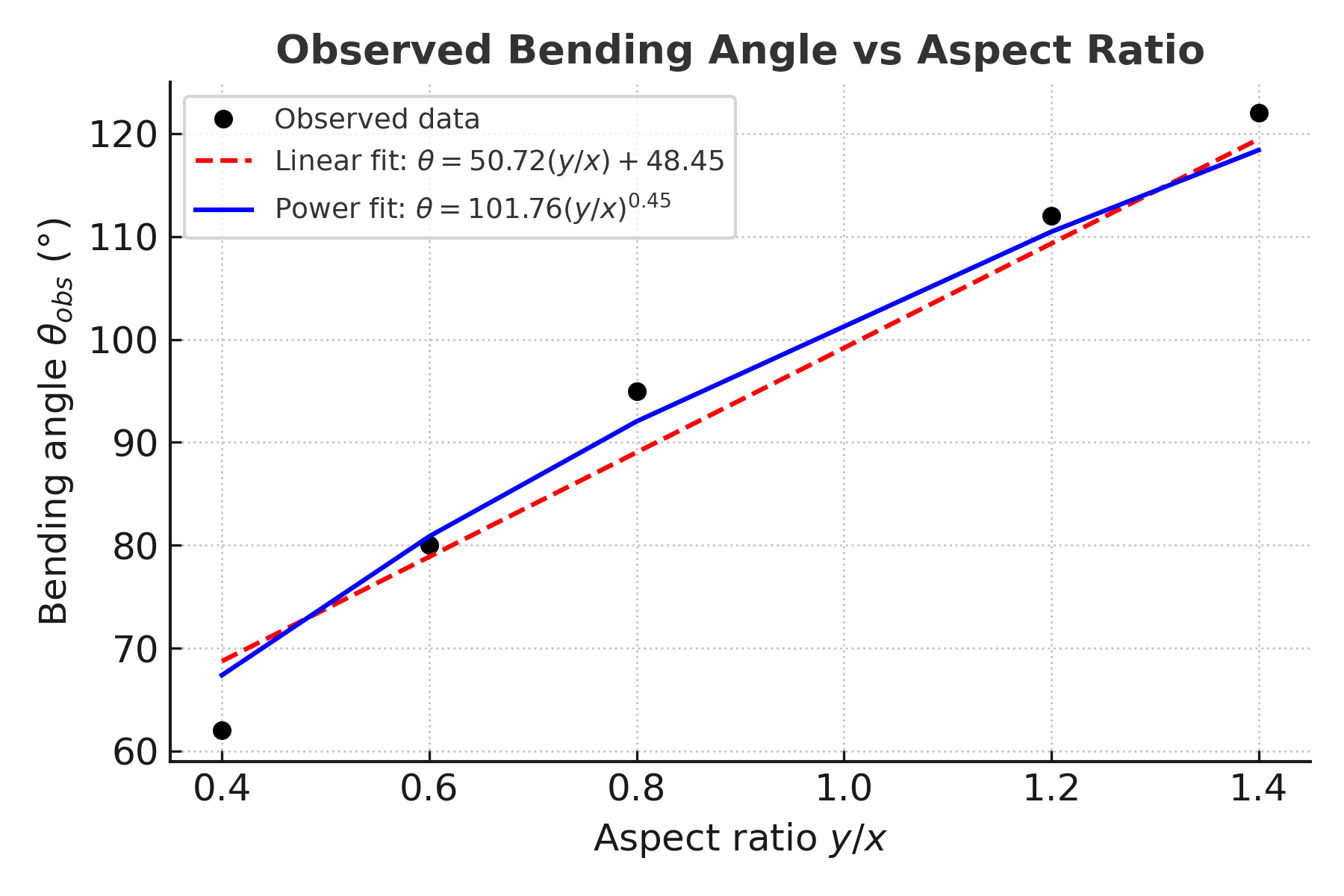
To make the comparison consistent, I scaled all designs to a pouch width of 10 cm, fixing the diamond’s $x$-axis at $8\ \text{cm}$ (0.8 × pouch width) and calculating the $y$-axis from the chosen $y/x$ ratios.
| $x\ \text{(cm)}$ | $y\ \text{(cm)}$ | $y/x\ \text{chosen}$ | $\theta_{\text{pred, linear}}\ (^\circ)$ | $\theta_{\text{pred, power}}\ (^\circ)$ |
|---|---|---|---|---|
| $8.0$ | $3.2$ | $0.4$ | $68.74$ | $67.30$ |
| $8.0$ | $4.8$ | $0.6$ | $78.88$ | $80.81$ |
| $8.0$ | $6.4$ | $0.8$ | $89.02$ | $92.01$ |
| $8.0$ | $9.6$ | $1.2$ | $109.31$ | $110.48$ |
| $8.0$ | $11.2$ | $1.4$ | $119.46$ | $118.44$ |